Surface differential geometry

Tools for surface differential geometry: maps between triangle meshes, map distortion, induced metric, vector calculus

When analyzing data in cartographic projections, we have to make sure we are always accounting for mapping distortion and curvature. This notebook builds the relevant tools, including for vector calculus on curved surfaces.

When analyzing quantities computed in the UV cartographic projection (e.g. cell areas, orientation, tissue flow speed obtained from optical flow), you need to account for the cartographic projection. I generally recommend doing this by mapping every object back to 3d as soon as possible. This will minimize the number of possible errors. Example: you want to evaluate the angle between two edges of a cell. 1. You could do so in the UV map using the induced metric (see below). This is error-prone: did you calculate the metric correctly? Did you use the metric or its inverse? 2. You could map back the location of the cell vertices to 3d, and then calculate the edge vectors in 3d. This minimizes possibilities for confusion.

Mapping distortion

A map between two meshes is defined on a per-triangle basis (i.e. which triangle of the “source” mesh gets mapped to which one of the “target” mesh). The map between a 3d mesh and its UV unwrapping is a special case of this.

The mapping distortion is described by the Jacobian, defined per triangle. For more details, see here. The simplest kind of mapping distortion is area distortion, which is simply the ratio of (target triangle area) / (source triangle area).

In general, many mapping-related quantities, like area distortion, are most easily computed per triangle. We can “move” them to mesh vertices by interpolation. If we keep all of our quantities of interest defined per vertex, it will simplify bookkeeping.

The tools in this notebook only work for triangular meshes! Only for triangular meshes is the per-face map distortion uniquely defined.

source

compute_per_vertex_area_distortion

 compute_per_vertex_area_distortion (source_vertices, source_faces,
                                     target_vertices, target_faces,
                                     evaluate_at='source', cutoff=1e-15)

*Compute area distortion factor for a map between meshes.

The result is evaluated at the vertices of the source or target mesh. Faces must be such that faces[i] is mapped to target_faces[i]. This function computes (target area / source area).

This can be used to (a) visualize map distortion and (b) correct for it, for example by using it as a weighting factor for averages.

Example (compute distortion of UV map): compute_per_vertex_area_distortion(mesh.texture_vertices, mesh.texture_tris, mesh.vertices, mesh.tris)*

Type Default Details
source_vertices np.array Source mesh vertices.
source_faces np.array of shape (…, 3) Spurce mesh faces. Must be triangular.
target_vertices np.array Target mesh vertices.
target_faces np.array of shape (…, 3) Target mesh faces. Must be triangular.
evaluate_at str source Whether to evaluate the result at the source or target
mesh vertices.
cutoff float 1e-15 Numerical cutoff for small target areas (avoid 0 division error)
Returns np.array Area distortion factor (source area/target area) evaluated on source or target mesh vertices.

source

impute_boundary_values

 impute_boundary_values (per_vertex_field, tris, fill_value=nan)

Replace values of per_vertex_field at boundary vertices by average of its non-boundary neighbors. If there are no non-boundary neighbors, use fill_value.

source

get_all_boundary_vertices

 get_all_boundary_vertices (tris)

Get list of all boundary vertices. Not guaranteed to be in any order

source

get_area_distortion_in_UV

 get_area_distortion_in_UV (mesh, uv_grid_steps=1024, map_back=True)

*Get area distortion of UV map, interpolated across the UV square.

Used to measure area distortion of your cartographic mapping. This can be used to (a) visualize map distortion and (b) correct for it, for example by using it as a weighting factor for averages.

Assumes the map \(x,y,z \mapsto u,v\) to be invertible. This is not guaranteed - you can create overlapping UV coordinates in blender. The provided UV coordinates will be mapped back to [0, 1]^2 if map_back is True. Else, coordinates outside [0,1] are ignored.*

Type Default Details
mesh tcmesh.ObjMesh Input mesh with UV coordinates.
uv_grid_steps int 1024 Size of UV grid. Determines resolution of result.
map_back bool True Map back the UV coordinates to [0,1]^2. Else, coordinates outside [0,1] are ignored.
Returns np.array of shape (uv_grid_steps, uv_grid_steps) Area distortion across [0,1]^2 UV grid, with uniform step size. UV positions that don’t
correspond to any value are set to np.nan.		 
mesh = tcmesh.ObjMesh.read_obj("datasets/movie_example/initial_uv.obj")
Warning: readOBJ() ignored non-comment line 4:
  o mesh_01_cylinder_seams_uv
distortion = compute_per_vertex_area_distortion(mesh.texture_vertices, mesh.texture_tris,
                                                mesh.vertices, mesh.tris)
plt.scatter(*mesh.texture_vertices.T, c=distortion, vmin=0, vmax=1e7, s=0.1)
plt.axis("equal")

distortion_interpolated = get_area_distortion_in_UV(mesh)
plt.imshow(distortion_interpolated, vmin=0, vmax=0.75*1e7)
/home/nikolas/Documents/UCSB/streichan/numerics/code/python_code/jupyter_notebooks/blender-tissue-cartography/blender_tissue_cartography/interpolation.py:217: RuntimeWarning: UV map has self-intersections, 33 flipped triangles. Try use_fallback=True?
  warnings.warn("UV map has self-intersections, {} flipped triangles. Try use_fallback=True?".format(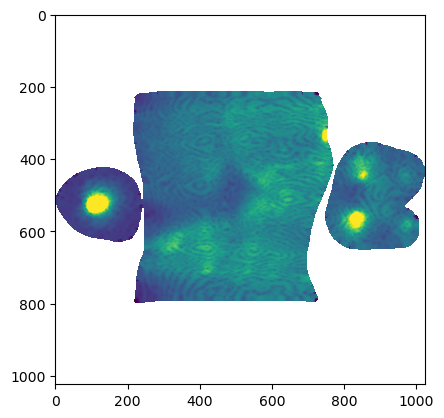

source

compute_per_vertex_angle_distortion

 compute_per_vertex_angle_distortion (source_vertices, source_faces,
                                      target_vertices, target_faces,
                                      evaluate_at='source', cutoff=1e-15)

*Compute angle distortion for a map between meshes.

The result is evaluated at the vertices of the source or target mesh. Faces must be such that faces[i] is mapped to target_faces[i]. This function computes np.abs(target angles - source angles), averaged over each triangle (in radians).

This can be used to visualize map distortion.

Example (compute distortion of UV map): compute_per_vertex_angle_distortion(mesh.texture_vertices, mesh.texture_tris, mesh.vertices, mesh.tris)*

Type Default Details
source_vertices np.array Source mesh vertices.
source_faces np.array of shape (…, 3) Spurce mesh faces. Must be triangular.
target_vertices np.array Target mesh vertices.
target_faces np.array of shape (…, 3) Target mesh faces. Must be triangular.
evaluate_at str source Whether to evaluate the result at the source or target
mesh vertices.
cutoff float 1e-15
Returns np.array Area distortion factor (source area/target area) evaluated on source or target mesh vertices. 
compute_per_vertex_angle_distortion(mesh.texture_vertices, mesh.texture_tris,
                                    mesh.vertices, mesh.tris).mean()
0.19397542576446897

Jacobian

In general, in addition to getting inflated or shrunk, during the mapping process, a triangle is also rotated and sheared. The full transformation properties are encoded by the Jacobian matrix.

You need the Jacobian for example to map vectors (e.g. displacement from optical flow) that you calculated in UV space back into 3d.

Using the tcinterp.interpolate_per_vertex_field_to_UV, you can interpolate the Jacobian from mesh vertices into the whole UV square.

source_vertices, source_faces = (mesh.texture_vertices, mesh.texture_tris)
target_vertices, target_faces = (mesh.vertices, mesh.tris)
A = source_vertices[source_faces]
B = target_vertices[target_faces]

A = (A.transpose((1,0,2)) - A.mean(axis=1)).transpose((1,0,2))
B = (B.transpose((1,0,2)) - B.mean(axis=1)).transpose((1,0,2))

A.shape, B.shape
((40420, 3, 2), (40420, 3, 3))
jac = np.stack([np.linalg.lstsq(a, b, rcond=None)[0].T for a,b in zip(A, B)]) # vectorize?

i = 100

np.linalg.norm(A[i] @ jac[i].T - B[i], axis=-1) / np.linalg.norm(B[i], axis=-1)
array([0., 0., 0.])

source

compute_per_vertex_jacobian

 compute_per_vertex_jacobian (source_vertices, source_faces,
                              target_vertices, target_faces,
                              evaluate_at='source')

*Compute Jacobian factor for a map between meshes.

Faces must be such that faces[i] is mapped to target_faces[i]. This function computes the Jacobian mapping tangent vectors of the source mesh to tangent vectors of the target mesh. The result is evaluated at the vertices of the source mesh.

Important: after you apply the per-vertex Jacobian, you may still need to permute the result, defined per source vertex, so it is defined per target mesh, e.g. using mesh.get_vertex_to_texture_vertex_indices() if mapping from 3d to UV.

Example (compute distortion of UV map): compute_per_vertex_jacobian(mesh.texture_vertices, mesh.texture_tris mesh.vertices, mesh.tris)*

Type Default Details
source_vertices np.array Source mesh vertices.
source_faces np.array of shape (…, 3) Spurce mesh faces. Must be triangular.
target_vertices np.array Target mesh vertices.
target_faces np.array of shape (…, 3) Target mesh faces. Must be triangular.
evaluate_at str source Whether to evaluate the result at the source or target
mesh vertices.
Returns np.array Jacobian. Shape is (n_vertices, d_target, d_source),
where d is the spatial dimension (e.g. 2, 3).

source

compute_per_face_jacobian

 compute_per_face_jacobian (source_vertices, source_faces,
                            target_vertices, target_faces)

*Compute Jacobian factor for a map between meshes.

Faces must be such that faces[i] is mapped to target_faces[i]. This function computes the Jacobian mapping tangent vectors of the source mesh to tangent vectors of the target mesh. The result is evaluated at the mesh faces.

Example (compute distortion of UV map): compute_per_vertex_jacobian(mesh.texture_vertices, mesh.texture_tris mesh.vertices, mesh.tris)*

Type Details
source_vertices np.array Source mesh vertices.
source_faces np.array of shape (…, 3) Spurce mesh faces. Must be triangular.
target_vertices np.array Target mesh vertices.
target_faces np.array of shape (…, 3) Target mesh faces. Must be triangular.
Returns np.array Jacobian. Shape is (n_faces, d_target, d_source),
where d is the spatial dimension (e.g. 2, 3).		 
jac = compute_per_vertex_jacobian(mesh.texture_vertices, mesh.texture_tris, mesh.vertices, mesh.tris)
jac.shape
(20623, 3, 2)
area_distortion = compute_per_vertex_area_distortion(mesh.texture_vertices, mesh.texture_tris,
                                                     mesh.vertices, mesh.tris)
# the product of the Jacobian singular values will give you the area distortion

np.prod(np.linalg.svd(jac).S, axis=1) / np.abs(area_distortion)
array([0.99769177, 0.99467172, 0.99815593, ..., 1.        , 0.99925048,
       1.        ])
jac = impute_boundary_values(jac, mesh.texture_tris, fill_value=np.nan*np.ones((3,2)))


jac_interpolated = tcinterp.interpolate_per_vertex_field_to_UV(mesh, jac, uv_grid_steps=256,
                                                               map_back=True, domain='per-texture-vertex')
plt.imshow(jac_interpolated[..., 0,1], vmin=-1e4, vmax=1e4)

Induced metric tensor

The induced metric is defined via \(g = J^T \cdot J\) where \(J\) is the Jacobian of the map from UV-space to 3d space.

Note: when doing calculations like those shown below, np.einsum is invaluable.

source

get_induced_metric

 get_induced_metric (mesh)

*Compute induced metric, evaluated at textures vertices.

See https://en.wikipedia.org/wiki/Induced_metric.*

Type Details
mesh tcmesh.ObjMesh Mesh. Must have texture map defined
Returns np.array of shape (n_texture_vertices, 2, 2) Induced metric.

source

get_metric_angle

 get_metric_angle (vf1, vf2, g)

Compute angle in radians between two vector fields (shape (…, d)) in degrees using metric g (shape (…, d, d)).

source

get_metric_norm

 get_metric_norm (vf, g)

Compute norm of vector field vf (shape (…, d)) using metric g (shape (…, d, d)).

# This is how you calculate the induced metric

jac = compute_per_vertex_jacobian(mesh.texture_vertices, mesh.texture_tris, mesh.vertices, mesh.tris)
g = np.einsum('via,vib->vab', jac, jac)
# The determinant of the metric gives the local area distortion
    
np.sqrt(np.linalg.det(g)) / np.abs(area_distortion)
array([0.99769177, 0.99467172, 0.99815593, ..., 1.        , 0.99925048,
       1.        ])
# Using the metric, and np.einsum, you can calculate norms and angles of vectors

vf = np.random.normal(size=jac[:,0].shape, scale=0.1)

np.sqrt(np.einsum('...i,...ij,...j->...', vf, g, vf))
array([  501.87392309,   393.09353282,   829.11721834, ...,
       25007.79899916, 56659.93322926, 97498.61554437])
mapped_to_3d = np.einsum('vij,vj->vi', jac, vf)
np.linalg.norm(mapped_to_3d, axis=-1)
array([  501.87392309,   393.09353282,   829.11721834, ...,
       25007.79899916, 56659.93322926, 97498.61554437])
jac.shape
(20623, 3, 2)

Vector calculus on curved surfaces

How to generalize the familiar operations of vector calculus (div, rot, grad, etc) to curved surfaces is a key part of differential geometry. There are different approaches for doing surface differential geometry numerically:

  1. Using local coordinates/parametrizations (i.e. the way physicists learn it in GR). This is prone to errors and numerically unfavorable
  2. Using “intrinsic” discretization schemes like Discrete Exterior Calculus. These are elegant and numerically efficient, but difficult to use and understand for non-experts.

Here, we take a less elegant, but simpler approach that takes advantage of the fact that our surfaces are embedded in 3d cartesian space. All vector and tensor fields are mapped back into 3d so that their components are defined in \(x,y,z\) coordinates. Then we can imagine “extending” from the surface into full 3d space by defining them to be constant along the local surface normal. Then we are back to normal vector calculus!

In practice, we don’t need to do this extension explicitly. We can compute the derivative of any quantity defined on mesh vertices in such a way that the derivative along the normal direction is 0. This is implemented by standard “finite-element” gradient operators. See here: https://libigl.github.io/libigl-python-bindings/tut-chapter1/#gradient

source

tri_grad

 tri_grad (field, vertices, faces, grad_matrix=None)

*Calculate the gradient of a function defined on vertices of a triangular mesh.

If a vector or tensor field is passed, the gradient is applied to each component individually.

See https://libigl.github.io/libigl-python-bindings/tut-chapter1/#gradient*

Type Default Details
field np.array of shape (#vertices,…) scalar, vector, or tensor field defined at mesh vertices
vertices np.array of shape (#vertices, dim) vertices.
faces np.array of shape (#faces, 3) Triangular faces.
grad_matrix NoneType None Gradient operator. The default is None (calculate from vertices, faces).
Returns np.array of shape (#vertices, dim, …) Gradient of scalar function/tensor, defined on vertices.
Axis 1 comprises the gradients along x,y,z.		 
mesh = tcmesh.ObjMesh.read_obj("datasets/movie_example/initial_uv.obj")
Warning: readOBJ() ignored non-comment line 4:
  o mesh_01_cylinder_seams_uv
# get some random fields - eigenfunctions of the laplacian

laplacian = igl.cotmatrix(mesh.vertices, mesh.tris)
mass = igl.massmatrix(mesh.vertices, mesh.tris)

eigen_vals, eigen_vecs = sparse.linalg.eigsh(-laplacian, M=mass, k=10, which="SM")
eigen_vals, eigen_vecs = (eigen_vals[1:], eigen_vecs[:, 1:])

eigen_vals = eigen_vals / eigen_vals[0]
eigen_vecs = eigen_vecs / np.abs(eigen_vecs).mean()

scalar_field = eigen_vecs[:,0]
vector_field = eigen_vecs[:,:3]
tensor_field = eigen_vecs.reshape((-1, 3, 3))
tri_grad(tensor_field, mesh.vertices, mesh.tris, ).shape
(20212, 3, 3, 3)
scalar_gradient = tri_grad(scalar_field, mesh.vertices, mesh.tris,)
normals = igl.per_vertex_normals(mesh.vertices, mesh.tris)
normals = (normals.T/np.linalg.norm(normals, axis=-1)).T
normal_component = (np.abs(np.einsum('vi,vi->v', normals, scalar_gradient))
                    / np.linalg.norm(scalar_gradient, axis=-1))
np.mean(normal_component)
0.0011230080906213756
# Here is how you would map the gradients to 2d. You first need to apply the Jacobian,
# and then you still need to reindex.

jac = compute_per_vertex_jacobian(mesh.vertices, mesh.tris, mesh.texture_vertices, mesh.texture_tris, )
scalar_gradient_projected = np.einsum('vij,vj->vi', jac, scalar_gradient)[mesh.get_vertex_to_texture_vertex_indices()]
plt.scatter(*mesh.texture_vertices.T, c=scalar_field[mesh.get_vertex_to_texture_vertex_indices()])

sk = 25
plt.quiver(mesh.texture_vertices[::sk, 0], mesh.texture_vertices[::sk, 1],
           scalar_gradient_projected[::sk, 0], scalar_gradient_projected[::sk, 1])

plt.axis("equal")

Projection onto surface normal

source

get_normal_projector

 get_normal_projector (vertices=None, faces=None, normals=None)

*Get projection matrix that removes components normal to the surface

Mathematically, 1-n.n^T where n is the unit surface normal. Defined per vertex.*

Type Default Details
vertices NoneType None vertices. If None, must supply normals
faces NoneType None Triangular faces. If None, must supply normals
normals NoneType None If None, recompute normals from vertices and faces
Returns np.array of shape (#vertices, dim, dim) Projector

source

separate_tangential_normal

 separate_tangential_normal (field, vertices=None, faces=None,
                             normals=None)

*Separate tangential and normal components of field defined at vertices.

Vector and rank-2 tensor fields are supported. For a rank-2 tensor, normal-tangential cross components are discarded.*

Type Default Details
field np.array of shape (#vertices, dim) or (#vertices, dim, dim) Vector or rank-2 tensor field defined at vertices
vertices NoneType None vertices. If None, must supply normals
faces NoneType None Triangular faces. If None, must supply normals
normals NoneType None If None, recompute normals from vertices and faces
Returns np.array, np.array tangential_component : np.array of shape (#vertices, dim) or (#vertices, dim, dim)
normal_component : np.array of shape (#vertices, dim) or (#vertices, dim, dim)		 
P = get_normal_projector(mesh.vertices, mesh.tris)
tangential, normal = separate_tangential_normal(vector_field, normals=mesh.normals)
np.einsum('vi,vi->v', tangential, mesh.normals), np.einsum('vi,vi->v', normal, mesh.normals)
(array([-0.00080435, -0.000788  , -0.00274249, ...,  0.00730656,
         0.0039478 ,  0.00005069]),
 array([-0.09762832, -0.09401892, -0.10817697, ...,  2.10673152,
         2.12017993,  0.08589414]))

div and rot

source

get_grad_perp

 get_grad_perp (field, vertices, faces, normals=None)

*Calculate the gradient of a scalar field, rotated by 90 deg around the surface normal.

As occurs e.g. when calculating vector field from stream function.*

Type Default Details
field np.array of shape (#vertices,) Scalar field defined at mesh vertices
vertices np.array of shape (#vertices, dim) vertices.
faces np.array of shape (#faces, 3) Triangular faces.
normals NoneType None If None, recompute normals from vertices and faces.
sign of normals determines sense of rotation.
Returns np.array of shape (#vertices, dim) 90-degree rotated gradient of scalar field.

source

get_rot

 get_rot (field, vertices, faces, normals=None)

*Calculate tangent-plane rotation of vector field defined on vertices of triangular mesh.

This result is a scalar, equal to (Nabla x field).normals*

Type Default Details
field np.array of shape (#vertices, dim) vector field defined at mesh vertices
vertices np.array of shape (#vertices, dim) vertices.
faces np.array of shape (#faces, 3) Triangular faces.
normals NoneType None If None, recompute normals from vertices and faces
Returns np.array of shape (#vertices,) Curl of vector field.

source

get_div

 get_div (field, vertices, faces, normals=None)

Calculate tangent-plane divergence of vector field defined on vertices of triangular mesh.

Type Default Details
field np.array of shape (#vertices, dim) vector field defined at mesh vertices
vertices np.array of shape (#vertices, dim) vertices.
faces np.array of shape (#faces, 3) Triangular faces.
normals NoneType None If None, recompute normals from vertices and faces
Returns np.array of shape (#vertices,) Divergence of vector field. 
get_div(vector_field, mesh.vertices, mesh.tris)
array([-0.00132147, -0.00133631, -0.00139445, ..., -0.01190545,
       -0.01149585, -0.00547986])
get_rot(vector_field, mesh.vertices, mesh.tris)
array([-0.00019284, -0.00021695, -0.00021081, ..., -0.00062418,
       -0.00052652,  0.00221077])